Front Row L-R: Mason Paccione, Teja Peddada, Sam Goldstein, Jake Sauter, Yue Xu
Back Row L-R: Ziniu Wu, Cara Van Uden, Joel Lee, Sheldon Lin, Momi Afelin, Rachel Schibler, Dawn Paukner, Quiana Jeffs, Ana Verma
Below is the 2018 Summer Undergraduate Research Program in Neuro Computation (uPNC) class roster. Selecting the name of the student will take you to a short description the the student’s research and link to their poster.
- Amber (Momi) Afelin
- Samuel Goldstein
- Quiana Jeffs
- Joel Lee
- Sheldon Lin
- Mason Paccione
- Dawn Paukner
- Teja Peddada
- Jake Sauter
- Rachel Schibler
- Cara Van Uden
- Ana Verma
- Ziniu Wu
- Yue Xu
The 2018 Summer Schedule can be downloaded here (pdf format).
Amber (Momi) Afelin
 Undergraduate Institution: Wesleyan University
Undergraduate Institution: Wesleyan University
Mentor: Pulkit Grover
University and Department: Carnegie Mellon University, Electrical and Computer Engineering
Project Description: Momi Afelin was involved in the group’s project of developing EEG systems for coarse and curly (e.g. African) hair. It is well-known issue that African Americans are unable to use today’s EEG system without treating their hair by steaming it. Moreover, steaming only works for a few tens of minutes. Because EEG is used in standard tests for epilepsy the issue is cause for significant clinical limitation.
Momi designed a novel electrode for EEGs for thick and curly hair, which built upon electrode designs previously designed by students in the group. We are currently testing these newly designed electrodes on African American participants.
Momi also worked on developing a wig for hiding EEG electrodes. This is particularly useful when someone suffering from a disorder (e.g. epilepsy) is being diagnosed using EEG, but does not want to reveal publicly that they are being tested.
Samuel Goldstein
 Undergraduate Institution: University of Florida
Undergraduate Institution: University of Florida
Mentor: Bard Ermentrout
University and Department: University of Pittsburgh, Mathematics
Project Description: When human subjects look at diffuse flickering light at particular frequencies, the visual field fills with geometric patterns such as hexagons, spirals and bullseyes. These so-called flicker phosphenes have been known about at least since Purkinje described them in his book. In a paper from 2011 Michael Rule (former uPNC student) and Ermentrout proposed a model for these based on the Wilson-Cowan equations that describe the behavior of a spatially coupled network of excitatory and inhibitory neurons. In this project, Sam Goldstein studied the effects of duty cycle (how long the light is on relative to how long it is off) on the stability of the cortical networks and also on how much the duty cycle affects the patterns that are seen in the model. We found that duty cycle has mixed effects on the stability — at high frequencies, the longer the light was on, the more the system became unstable while at low frequency stimulus, there was an optimal duty cycle for instability. For high frequency, the duty cycle had little effect on the patterns observed, while at low frequency, the patterns varied widely.
Quiana Jeffs
 Undergraduate Institution: University of Texas at Austin
Undergraduate Institution: University of Texas at Austin
Mentor: Rob Kass
University and Department: Carnegie Mellon University, Statistics
Project Description: Previous work, including in Matt Smith’s Lab here in Pittsburgh, has shown that the correlation between spike counts from a pair of neurons tends to decrease as the distance between the neurons increases. In this project we examined the extent to which a similar phenomenon holds for phase coupling. Phase coupling refers to a consistent phase relationship in a pair of neural oscillations. Substantial circumstantial evidence has pointed to a role for neural oscillations in cognitive processes. Phase coupling of a pair of neural signals would represent a form of communication between the regions from which the signals were recorded. Quiana Jeffs analyzed local field potentials (LFP) from 96 electrodes collected with a Utah array in visual area V4 by the Smith Lab. LFPs were band-pass filtered at 15 Hz, corresponding to beta oscillations. We applied the widely-used phase coupling measure known as Phase Locking Value (PLV). We found a clear decreasing relationship of PLV with increasing distance between the electrodes. Please see the description of the closely related project of Joel Lee.
Joel Lee
 Undergraduate Institution: University of California at Berkeley
Undergraduate Institution: University of California at Berkeley
Mentor: Rob Kass
University and Department: Carnegie Mellon University, Statistics
Project Description: Previous work, including in Matt Smith’s Lab here in Pittsburgh, has shown that the correlation between spike counts from a pair of neurons tends to decrease as the distance between the neurons increases. In this project we examined the extent to which a similar phenomenon holds for phase coupling. Phase coupling refers to a consistent phase relationship in a pair of neural oscillations. Substantial circumstantial evidence has pointed to a role for neural oscillations in cognitive processes. Phase coupling of a pair of neural signals would represent a form of communication between the regions from which the signals were recorded. Joel Lee’s project was closely related to the project of Quiana Jeffs. We analyzed local field potentials (LFP) from 96 electrodes collected with a Utah array in visual area V4, and another array in Prefrontal Cortex (PFC) by the Smith Lab. LFPs were band-pass filtered at both 10 Hz and 15 Hz, corresponding to alpha and beta oscillations, respectively. We applied the widely-used phase coupling measure known as Phase Locking Value (PLV). In both regions, and for both frequencies, we found a clear decreasing relationship of PLV with increasing distance between the electrodes. The relationship was not affected by total power in the signal. PLV was stronger in V4 than in PFC. We did not find phase coupling across the two regions.
Sheldon Lin
 Undergraduate Institution: University of Pittsburgh
Undergraduate Institution: University of Pittsburgh
Mentor: Aaron Batista
University and Department: University of Pittsburgh, Bioengineering
Mason Paccione
 Undergraduate Institution: Carnegie Mellon University
Undergraduate Institution: Carnegie Mellon University
Mentor: Rob Kass
University and Department: Carnegie Mellon University, Statistics
Project Description: In recent decades, much work has been done in the modeling of individual neurons and network connections. This has made it possible to generate neural spiking data that resembles real neural data, while controlling an underlying generative process. In this project Mason Paccione used a particular software platform, the NENGO Neural Simulator, to create a “ground truth” with which we can evaluate statistical methods for identifying network structure. Individual neurons are modeled essentially as integrate-and-fire neurons, except that they fire probabilistically, which allows us access to ground truth instantaneous firing rates. The goals of this work are, first, to build models for multiple brain areas having interesting dynamics, and dynamic interactions; second, to build statistical methods for determining dynamic interactions; and third, to evaluate the statistical methods using the model-based ground truth simulator.
Dawn Paukner
 Undergraduate Institution: University of Wisconsin
Undergraduate Institution: University of Wisconsin
Mentor: Brent Doiron
University and Department: University of Pittsburgh, Mathematics
Teja Peddada
 Undergraduate Institution: University of Pittsburgh
Undergraduate Institution: University of Pittsburgh
Mentor: Steve Meriney
University and Department: University of Pittsburgh, Neuroscience
Project Description: In the summer of 2018, Teja Peddada was focused on advancing or understanding of how the nerve terminal controls the release of chemical transmitters. As a model system, he used the frog neuromuscular junction (NMJ) synapse, and some of our “wet lab” data to constrain a computer model of nerve terminal function. In particular, he modeled the manner by which an electrical depolarization of the nerve terminal (an action potential) caused the gating of two types of ion channels (voltage-gated calcium channels and calcium-activated potassium (BK) channels). While we have know that these channels exist in the motor nerve terminal for some time, the precise manner by which they work together to control the transmitter output of the synapse is not known. Little is known about the BK channel’s structure-function relationship with calcium channels and docked synaptic vesicles. Studying BK channel effects on the calcium ion entry and the action potential waveform is crucial to the overall understanding of the NMJ and neuromuscular diseases such as Lambert-Eaton myasthenic syndrome (LEMS) in which there is a reduction in the number of presynaptic calcium channels in the AZ. To study these relationships, we used a recently developed computer model using MCell, which is an optimized stochastic reaction-diffusion simulation software used to accurately model biological systems. According to the model, blocking BK channels is predicted to nearly double the probability of neurotransmitter release compared to the control action potential waveform. These studies will allow us to combine MCell with the software NEURON in the future to predict changes in action potential shape due to BK channel activation, and the resulting effects on transmitter release. These data will be compared and constrained by physiological recording. Overall, these data will significantly advance our understanding of motor nerve terminal function in healthy and diseased states.
Jake Sauter
 Undergraduate Institution: State University of New York at Oswego
Undergraduate Institution: State University of New York at Oswego
Mentor: Marc Coutanche
University and Department: University of Pittsburgh, Psychology
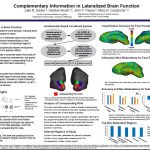
Project Description: Jake Sauter developed an anatomically based coordinate system that can be used to investigate lateralized processing in brain activity collected through functional magnetic resonance imaging (fMRI). This coordinate system was used to guide a surface-based exploratory searchlight, in which multi-voxel activity patterns were analyzed with machine learning classifiers to decode the type of stimulus viewed by a subject. The anatomical coordinate system was then used to identify left and right homologous regions of interest. Finally, classification performance in lateralized regions and their combination were systematically compared, in order to measure the degree of information non-redundancy across hemispheres.
Rachel Schibler
 Undergraduate Institution: Harvey Mudd College
Undergraduate Institution: Harvey Mudd College
Mentor: Matt Smith
University and Department: University of Pittsburgh, Ophthalmology
Project Description: The activity of neurons in sensory regions of the brain is driven by both external sensory stimuli and by internal cognitive states. To understand the neural code for our perceptual experience, we must separately understand how these external and internal influences shape neural activity. However, measuring an internal cognitive state is challenging, particularly in the face of limited access to only a small handful of the neurons that give rise to such a state. One potential solution to this problem comes in the form of multiscale recordings which take advantage of the information provided by networks of neurons across the brain. Rachel analyzed large-scale electrophysiological recordings from non-human primate visual and prefrontal cortex and related a slow time scale fluctuation in the activity of neuronal populations to fluctuations in the behavior of the animal. She then analyzed concurrently recorded electroencephalography (EEG) signals from the scalp to gauge the same underlying state variables, demonstrating that neurally-based estimates of internal states can be reached non-invasively.
Cara Van Uden
 Undergraduate Institution: Dartmouth College
Undergraduate Institution: Dartmouth College
Mentor: Marcel Just
University and Department: Carnegie Mellon University, Psychology
Project Description: Cara Van Uden’s project decoded the emotional content of the brain activation patterns observed during an fMRI-measured resting state. She compared resting-state emotional content across several clinical groups whose fMRI resting-state data were publicly available. The data were from nearly 300 people, across four clinical groups (suicidal ideators, bipolar disorder, schizophrenia, ADHD) and a control group. There were two main components to her work.
The first part of her work (consuming several weeks) was to find and tune segmentation algorithms that divided a 5-minute resting state dataset into approximately 15 successive time segments. The goal was to identify segments within which the mental state was fairly stable (as assessed with functional connectivity measures (Xu & Lindquist, 2015)).
The second part of her work was to match previously-obtained template activation patterns for 9 emotions (e.g. anger, envy, happiness, sadness) to the resting state data in each time window (that was indicated by the segmentation process). The templates consisted of mean activations in 29 ROIs (Kassam et al 2013).
The results were that there were statistically reliable differences between clinical groups with respect to the emotions they exhibited. For example, the schizophrenia patients experienced emotions more intensely, particularly envy.
The most significant outcome of Cara’s project is the demonstration that the content of thought during a resting state (the most common type of fMRI acquired) is amenable to decoding and hence potentially diagnostic of mental disorders.
Ana Verma
 Undergraduate Institution: Amherst College
Undergraduate Institution: Amherst College
Mentor: Alison Barth
University and Department: Carnegie Mellon University, Biology
Project Description: Ana Verma used high-resolution, volumetric confocal images for automated, fluorescence-based detection of inhibitory synapses in the cerebral cortex. Using sparse expression of novel fluorescence tags that label postsynaptic sites with high fidelity, Ana could identify spiny dendritic segments and their synapses on neocortical pyramidal neurons and then digitally align these synapses with afferents from different classes of neocortical GABAergic neurons, specifically somatostatin and parvalbumin-expressing cells. Ana tested the detection algorithm using a range of distance detection parameters and also across different cortical layers where the density of labeled presynaptic afferents varied several-fold.
Ziniu Wu
 Undergraduate Institution: Carnegie Mellon University
Undergraduate Institution: Carnegie Mellon University
Mentor: Tai-Sing Lee
University and Department: Carnegie Mellon University, Computer Science Department
Project Description: While deep convolutional neural networks (DCNN) can provide state-of-the-art model for predicting neurons’ responses to complex images, the filters learned are often not easily interpretable. Ziniu Wu explored the idea whether filters or code dictionaries learned based on efficient coding criteria can be used as a front end to build better and more interpretable CNN for predicting neural responses. He found that the dictionaries learned using unsupervised learning based on efficient coding principles can indeed help build better models both for projection pursuit regression method and convolutional neural network method. This finding provides further evidence in support of the sparse coding principle, as well as provides more interpretable constituting components of the receptive fields of the neurons.
Yue Xu
 Undergraduate Institution: Carnegie Mellon University
Undergraduate Institution: Carnegie Mellon University
Mentor: Tai-Sing Lee
University and Department: Carnegie Mellon University, Computer Science Department
Project Description: Yue Xu investigated the connections between scene statistics and neuronal codes at the individual level and at the population level. Specifically, she evaluated whether neuronal population codes for more frequently occurring image patterns is more sparse than those for less frequently occurring patterns. As no two image patterns would be exactly alike, the frequency of occurrence of an image pattern depend on the metric of similarity. Yue investigated the embedding space of different layers of a deep neural network and found that the layer that is most representationally similar to the neural representation in V1 also exhibits the highest correlation between sparsity and frequency, controlled for the complexity of the image patterns. In this embedding space, the more frequently occurring image patterns indeed are sparser in their population response representation. This provides empirical evidence for the efficiency of neural codes.

